Foamy complex matter is increasingly encountered in various application fields. During the PhD thesis of François Gorlier (2014-2017), we considered two different types of complex matter to be mixed with aqueous foam and we investigate the resulting rheology (elastic modulus and yield stress): (1) a concentrated emulsion possessing intrinsic elastic and yield stress properties, and (2) granular suspensions which are known to exhibit particle size effects when incorporated into foam.
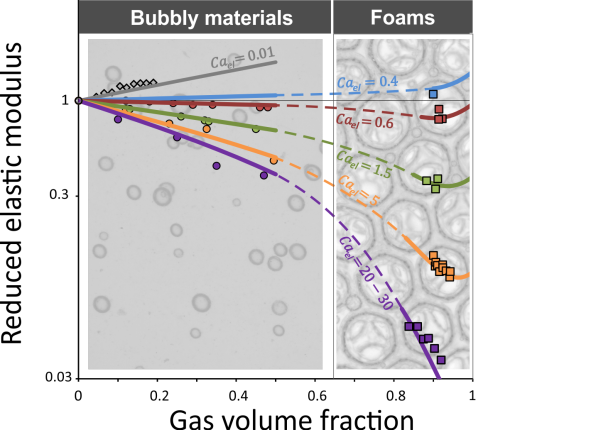
We elaborated well-controlled foams with concentrated emulsion and we measured their shear elastic modulus as a function of gas fraction, bubble size and elastic modulus of the emulsion. Such complex foams possess the elastic features of both the bubble assembly and the interstitial matrix. Moreover, their elastic modulus was shown to be governed by two parameters, namely the gas volume fraction and the elasto-capillary number, defined as the ratio of the emulsion modulus with the bubble capillary pressure. We connected our results for foams with existing data for bubbly systems and we provide a general view for the effect of gas bubbles in soft elastic media.
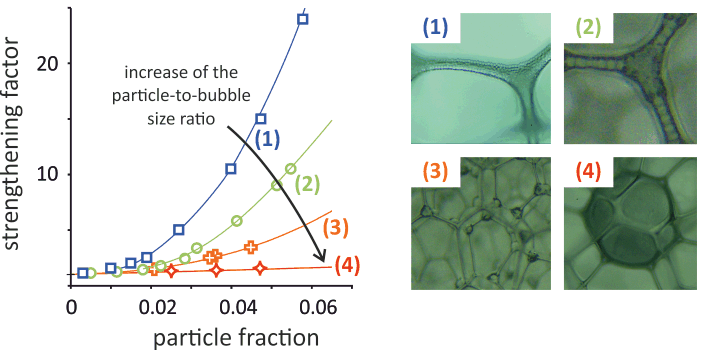
We generated well-controlled particle-loaded liquid foams and we determine their elastic behavior as a function of particle size (6-3000 µm) and particle volume fraction (0-6%). We focused on both the elastic modulus exhibited by the material at small strain and the strain marking the end of the linear elastic regime. Results revealed the existence of a critical particle-to-bubble size ratio triggering a sharp transition between two well-defined regimes. For small size ratios, the behavior is governed by the mechanical properties of the solid grains, which have been proved to pack in the shape of a foam-embedded granular skeleton. In contrast, bubbles elasticity prevails in the second regime, where isolated large particles contribute only weakly to the rheological behavior of the foamed material. The modeling of elasticity for each regime allows for this transition to be normalized and compared with previously reported particle size-induced effects for foam drainage (Haffner et al. J. Colloid Interface Sci., 2015, 458, 200–208) and solid foam mechanics (Khidas et al., Compos. Sci. Technol., 2015, 119, 62–67). This highlighted that rheology and the other properties of particle-loaded foams are subjected to the same size-induced morphological transition.
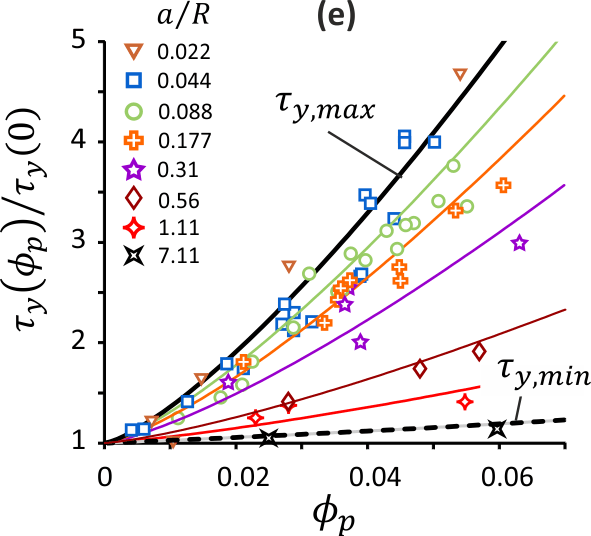
Yield stress of emulsion foams is found to be governed by both the Bingham-capillary number (i.e. the emulsion yield stress scaled by the bubble capillary pressure), and the volume fraction of interstitial emulsion. Foams made with small solid particles reveal granular packings confined between foam bubbles and the resulting yield stress is shown also to be governed by the Bingham-capillary number, here based on Mohr-Coulomb criterion applied to the interstitial granular material. Yield stress of foams made with large particles is well-described by theory developed from micro-mechanics of particle-loaded yield stress materials, suggesting that for such size ratios, foam can be considered as a continuous matrix. Within the range of intermediate size ratio values the normalized foam yield stress undergoes an exponential decay that seems to be related to the number of bubbles separating neighboring particles. Finally, reported results are used to estimate the thicknesses of foamed material, such as isolating foamed mortars for example, that can be deposited on vertical substrates.
Related papers:
– Optimal strengthening of particle-loaded liquid foams, F. Gorlier, Y. Khidas, A. Fall, O. Pitois, Physical Review E (2017) 95, 042604 (I. Factor 2,315)
– Elasticity of particle-loaded liquid foams, F. Gorlier, Y. Khidas, O. Pitois, Soft Matter (2017) 13, 4533-4540 (I. Factor 3,889)
– Coupled Elasticity in soft solid foams, F. Gorlier, Y. Khidas, O. Pitois, Journal of Colloid and Interface Science (2017) 501, 103-111 (I. Factor 3,988)
– Yielding of complex liquid foams, F. Gorlier, Y. Khidas, O. Pitois, Journal of Rheology (2017) 61, 919 (I. Factor 3,136)


