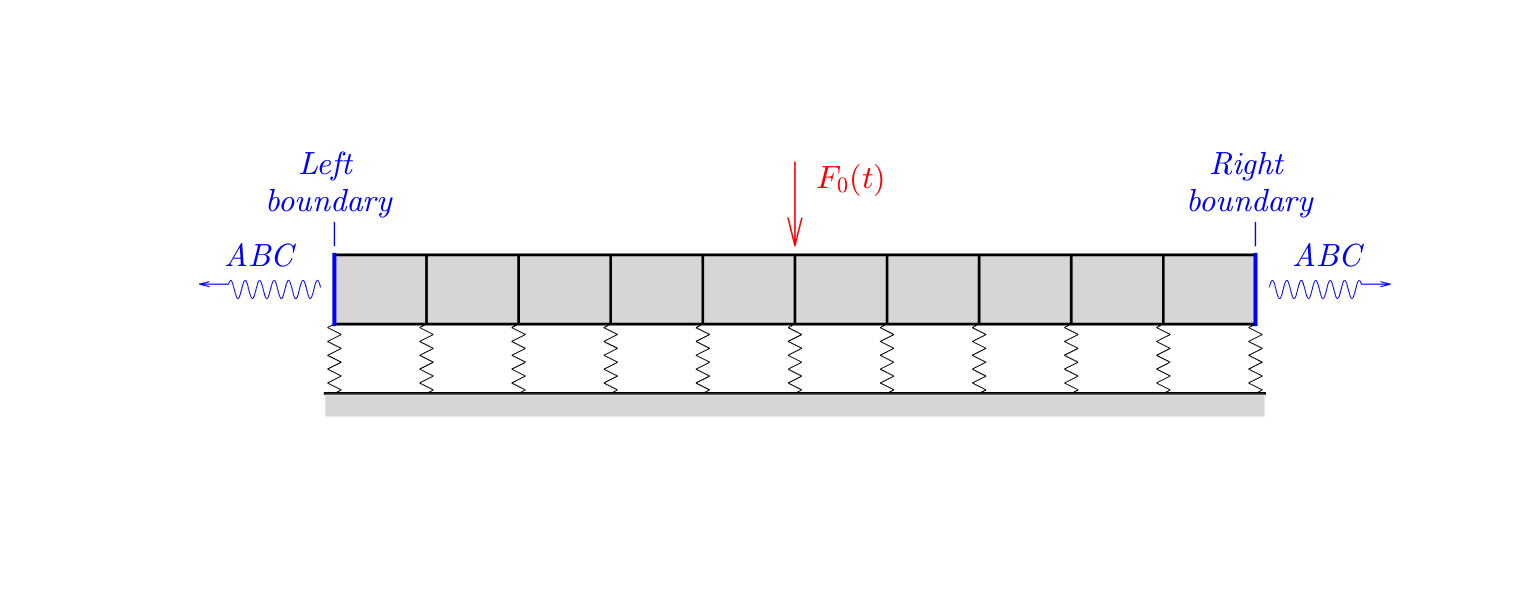
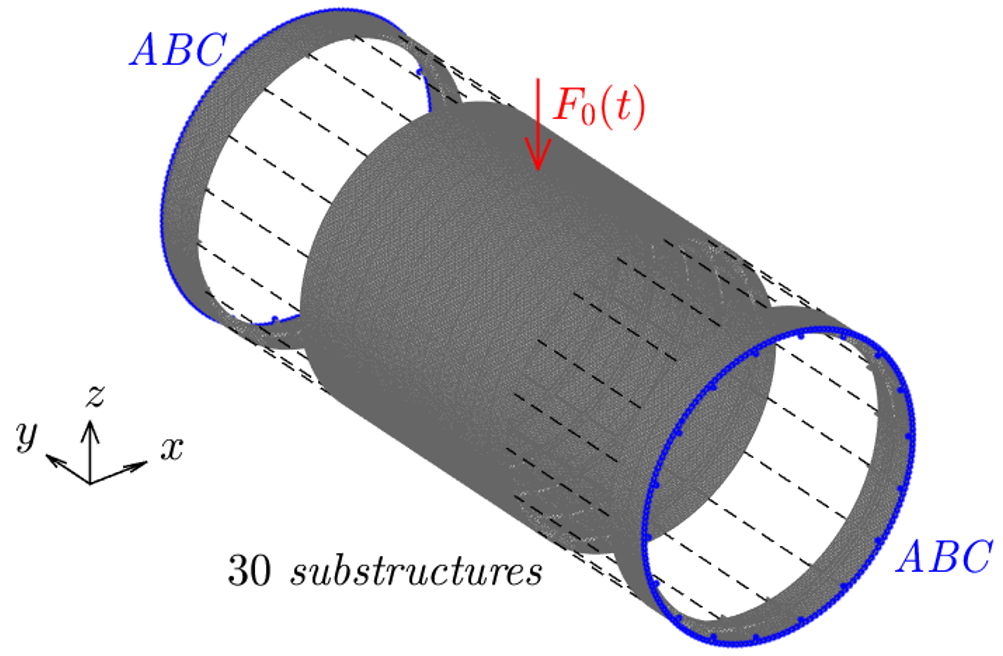
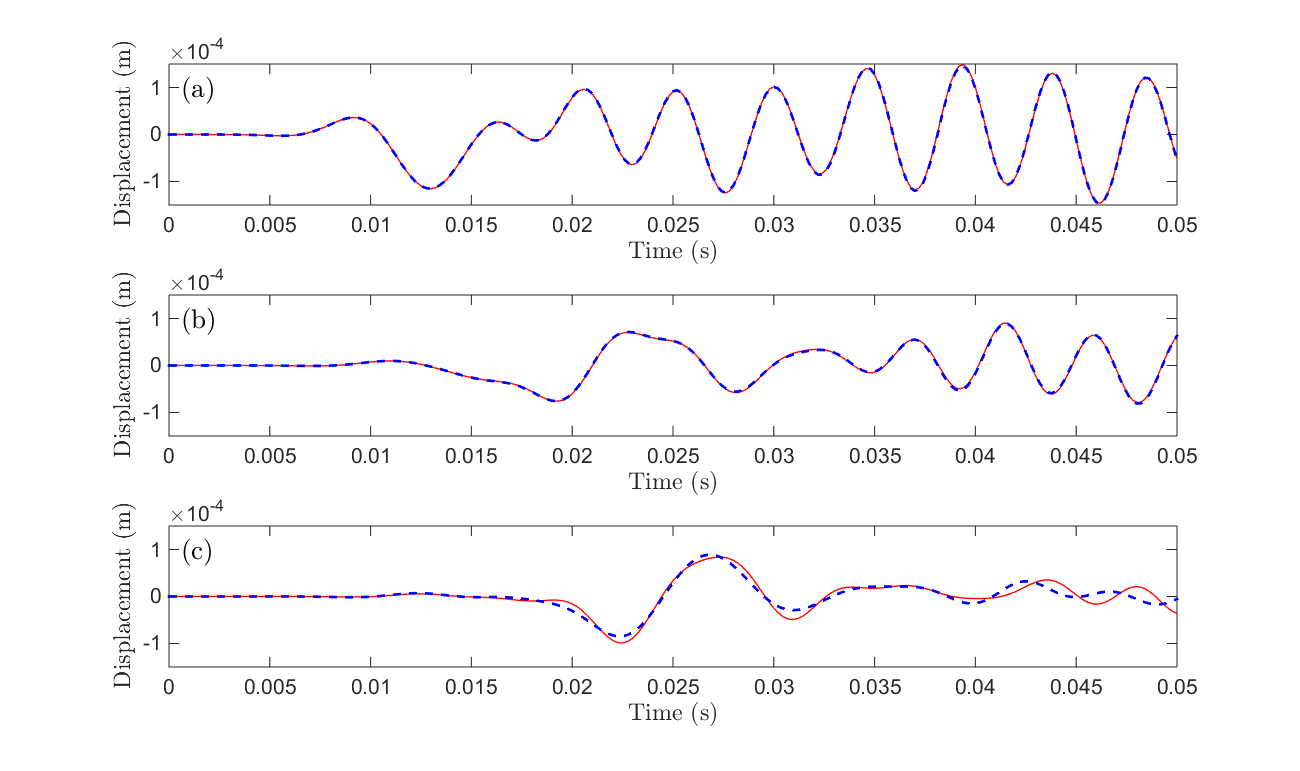
Cette activité se concentre autour de la méthode Wave Finite Element (WFE) dont le principe est de décrire la propagation des ondes harmoniques dans un milieu périodique (image ci-dessous à gauche) à partir des ondes dans une seule cellule en utilisant le théorème de Floquet. Les principales avancées récentes ont concerné la possibilité de décrire le mouvement avec un nombre réduit de modes d’onde et la prise en compte de chargements complexes. Par ailleurs, alors que la méthode est à l’origine formulée dans le domaine fréquentiel, une modélisation d’un domaine périodique fini a été proposée dans le domaine temporel avec des conditions aux limites absorbantes aux extrémités. Les développements actuels sur ce dernier point visent à améliorer la méthode en utilisant la méthode de Craig-Bampton pour réduire les degrés de liberté internes aux cellules dans le cas de structures complexes (image ci-dessous au centre) et à réduire aussi les degrés de liberté aux interfaces entre les cellules. La comparaison avec un calcul éléments finis classique sur un grand domaine (image ci-dessous à droite) montre l’intérêt de la méthode pour réduire la taille du domaine utilisé dans la modélisation.

Les applications pratiques de la WFE sont par exemple la dynamique des voies ferroviaires et les vibrations de ponts. L’image suivante montre un calcul de voie ferrée dans lequel le comportement de toute une voie sous une charge mobile (à droite)  peut être obtenu par la WFE à partir d’un calcul fait sur une seule portion de voie (à gauche).

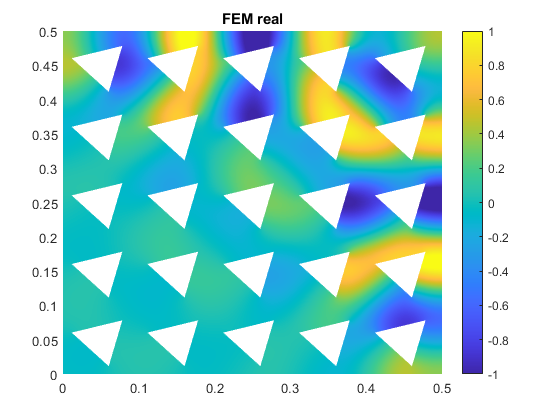
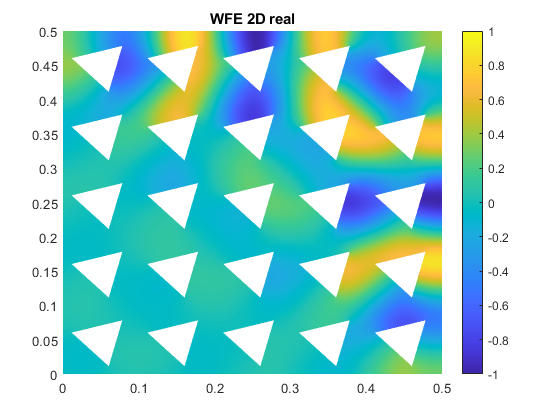
Le cas d’une périodicité suivant deux directions est également exploré et une méthode efficace a été proposée pour calculer la réponse à une excitation externe d’un milieu périodique 2D comportant un grand nombre de cellules par WFE (image ci-dessous à droite) avec le même résultat qu’un calcul élément fini classique modélisant toute la structure (image ci-dessous à gauche).