Granular media, which are materials composed by grains, are a good model for soils. Their mechanical properties should be properly described for civil engineering and geophysics applications.

We are interested in understanding how the mechanical and flowing properties of granular media are affected by their structure at different length scales.

For this, we use different experimental methods, such as X-ray microtomography, MRI,  acoustic waves, optical image correlation, providing insights on the nature of the contacts and the arrangements of the grains.

The mechanical and flowing properties of the granular systems with controlled structures are studied by means of rheometers and inclined planes.

Numerical simulations (DEM) provide information not available from experiments and allow building a complete set of data for modelling.

Rheology and structure of granulars

A. Fall, J.-N. Roux, F. Chevoir, A. Awdi (PhD), C. Chateau (ME)
Collaborations : S. Debœuf (d’Alembert)

The study of the rheology of granular materials in shear flow has been an area of research for the team since the early 2000s. The granular group of our laboratory is among the pioneers of “µ(I) rheology”. In this approach, the state of the material in stationary flow under imposed lateral stress, and therefore free to adapt its density, generalizes the critical state known in geomechanics and, when the elastic deflexion of the contacts remains suffisufficiently low, depends only on the inertial number I, defined as the shear rate adimensionalized by an inertial characteristic time at the grain scale under pressure P. Rheological laws then express the compactness of the granular assembly Φ and the coefficient of internal friction µ* (as well as normal stress differences) as functions of I.

Much of the most recent research has focused on the rheology of cohesive granular materials, particularly when this cohesion is of capillary origin, caused by the presence of liquid bridges joining grains in contact or in close proximity. Constitutive relations can then be formulated which generalize the “µ(I) rheology” by involving, in addition to the inertial number I, the reduced pressure P* defined from grain diameter d, controlled stress P and attractive intergranular force F0 (proportional to d and interfacial tension in the case of capillary cohesion) as P*= Pd^2 /F0

Measurement of the water content of an unsaturated granular medium by X-ray microtomography. (a) X-ray microtomograph and inserted geometry (b) Cross-section of the shear cell. (c) Translation and rotation stages forming the bottom of the shear cell.

 

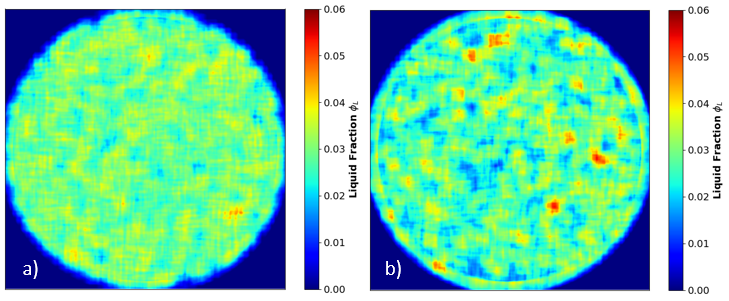
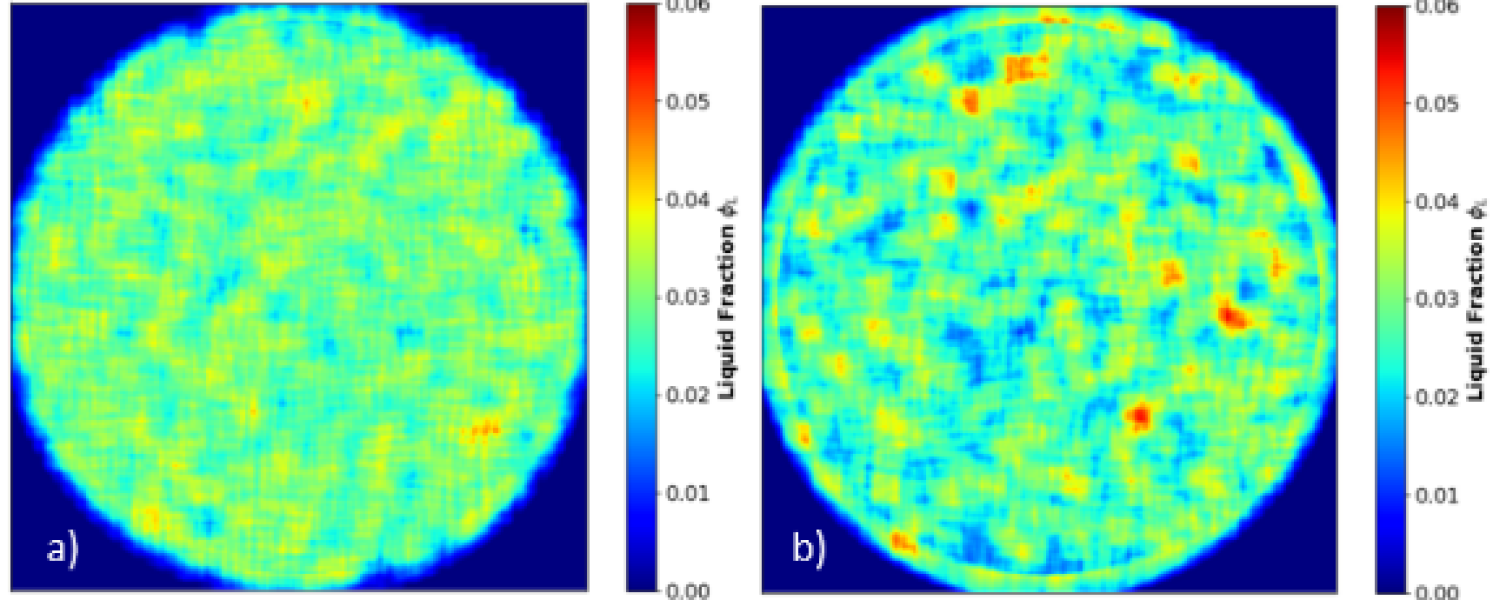
Cross-sectional view of the water content of an unsaturated granular medium, (left) in its initial state, (right) after 10 minutes of shearing.

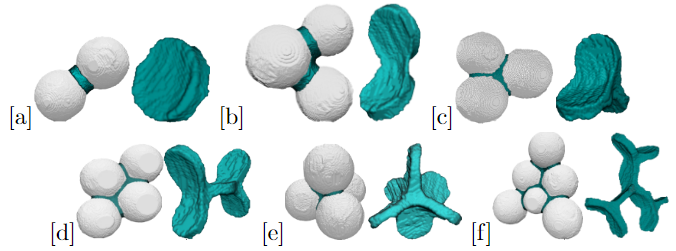
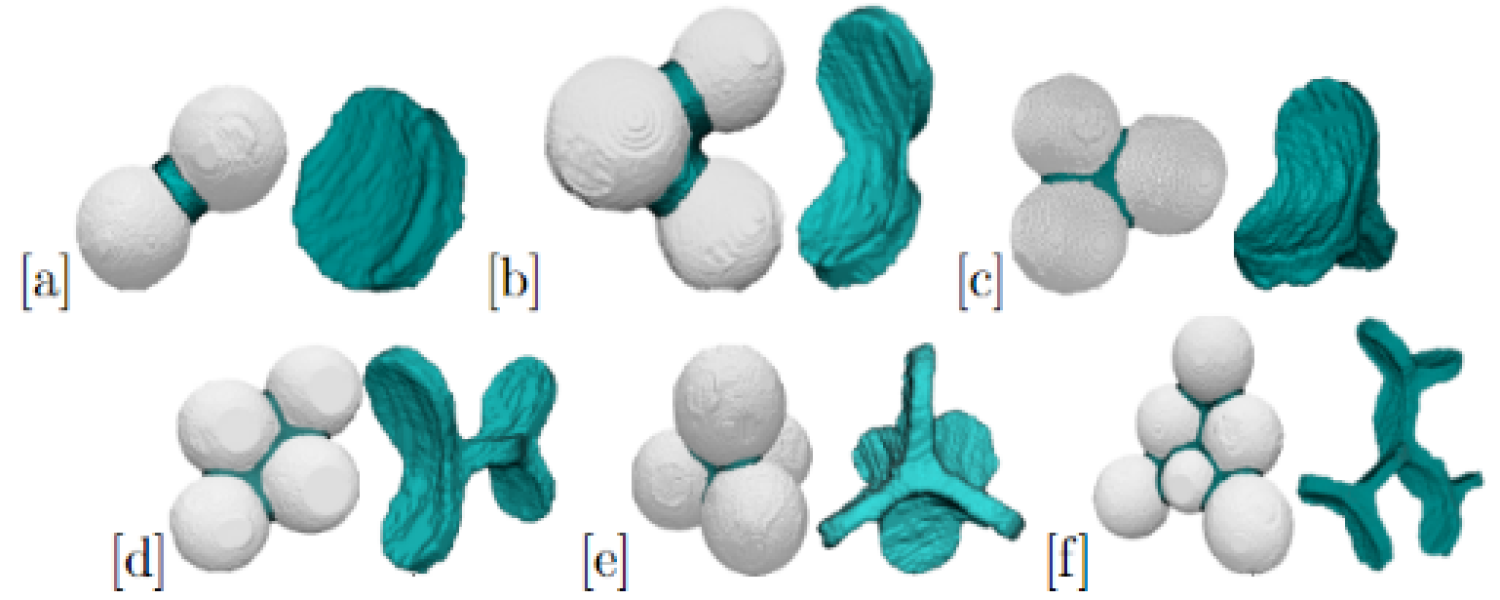
Liquid bridges and more complex interstitial water morphologies between pairs (triplets, quadruplets, …) of grains.

 

References

Granular materials in quasi-static deformation

J.N. Roux, A. Fall, F. Chevoir

The quasi-static regime, for solid granular materials, can be approximated in the limit (I → 0) of slow flows. The numerical study of unsaturated model materials then allows us to revisit the notions of cohesion in the Mohr-Coulomb sense. These same model materials can be presented in very loose states, analogous to colloidal gels, and are the subject of systematic numerical studies in isotropic or triaxial compression.

In Fig. 1, model granular assemblies and force networks in two-dimensional equilibrium under isotropic pressure illustrate the difference between cohesive structures, which can be very open and porous, and cohesionless states of granular materials.

For a general study of their quasi-static behavior (considered representative of that of cohesive materials such as powders), numerical simulation studies have adopted an ideal, homogeneous and isotropic method of assembly, in which grains isolated from a loose medium, animated by a random velocity distributed according to Maxwell’s law, gradually form, by ballistic aggregation, at a volume kept constant, a kind of gel (Fig. 2). This structure gradually reaches mechanical equilibrium, as collisions and intergranular friction dissipate kinetic energy.

The initial loose structure will progressively collapse when an increasing stress is applied to it, in isotropic or oedometric compression (Fig. 3). In geomechanics, this compression is traditionally expressed by the variation in void index e = (1 – Φ)/Φ, the ratio of void volume to grain volume. Starting from a loose state of compactness Φ = 0.3 for figure 3 (right) (e approx 2.33), we observe an irreversible compression to a final state whose density is similar to that of the loosest cohesionless assemblies (e approx 0. 732 or Φ approx 0.577, the coefficient of intergranular friction here being 0.3), with very little change on decompression (see the arrows on the graphs).

We can see that irreversible isotropic compression behavior depends on the initial state via its density (Fig. 3, left) and also on its structure, determined in particular by the intensity of agitation during ballistic aggregation (Fig. 3, right). These observations contradict certain notions relating to cohesive soils, in particular the property, classic in geotechnical literature, that in the plastic phase of compression, the coordinate points (ln P, e) form a single curve.

Fig. 1

Left: typical appearance of an assembly of circular grains under isotropic pressure, the ‘chains of forces’ ‘etant represented as usual by segments joining neighbors with a ‘line thickness proportional to the intensity of the normal force.

Right: loose state stabilized by cohesion, repulsive forces are figured in red, attractive forces in green, contacts where attraction is compens’ee by elastic repulsion (zero total normal force) are in blue.

 

Fig. 2 Loose assembly of cohesive beads (compactness Φ = 0.3), by ballistic aggregation. Left: low initial agitation, such that adhesive contacts do not break. Right: with high initial agitation, contacts can open, aggregates rearrange, producing a structure with stronger heterogeneities (dense and void regions). These images show a slice with a thickness equal to three diameters.

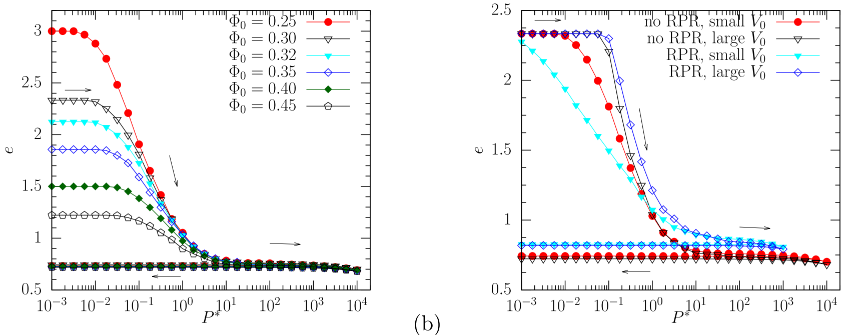
Fig. 3 Void index as a function of reduced pressure P* (logarithmic scale) for different u=initial states, of different compacity Φ0 (left), or with different velocities during the initial ballistic aggregation process (right), for Φ0 = 0.3. The second plot also shows the influence of rolling and pivoting resistance (RPR), with µR = µP = 0.02a.

 

References

  • J.N. Roux, M. H. Khalili, F. Froiio, and C. Dequeker. Elasticity and Mechanical Behaviour of Granular Materials : Some Insights from Numerical Studies of Simple Systems. In Views on Microstructures in Granular Materials, volume 44 of Advances in Mechanics and Mathematics, pages 185–224. Springer International Publishing, November 2020.
  • V.-D. Than. Compression behavior of loose wet granular materials : experiments and discrete numerical simulations. Thèse de doctorat (Université Paris Est), 2017.