

Context: In mechanical engineering or material science, interfaces are where the magic – and the challenges – happen. From the layers in composite materials to the bonds in biological tissues, interfaces often determine whether a material thrives under stress or fails catastrophically. Designing tough interfaces – ones that can resist cracking while absorbing and dissipating energy – is a cornerstone of creating durable materials.
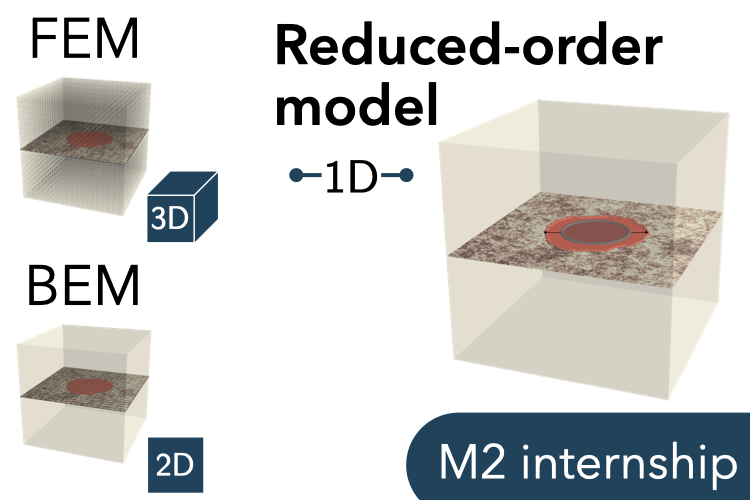
To make interfaces tougher, we often need to introduce heterogeneities — controlled variations in fracture or elastic properties – to disrupt crack propagation. Instead of a crack traveling straight through, it must navigate obstacles, detour, arrest, and absorb/dissipate energy along the way. This mechanism mimics strategies found in nature, such as in nacre or bone, where alternating layers or structural imperfections are present at multiple hierarchical scales to create remarkable toughness without sacrificing strength. However, simulating 3D crack growth with standard finite-element (FEM) or boundary-element (BEM) methods is challenging as it requires fine meshing of the whole 3D elastic body (for FEM) or 2D interface (for BEM), especially near the propagating crack front where stress are concentrated. To address this issue, remeshing techniques, enriched crack tip elements, or diffuse damage models have been proposed. Yet, the numerical cost associated with these methods do not permit to model failure process from the scale of the heterogeneity to that of the structure, especially when material microstructure contains several – hierarchical – scales of heterogeneities.
Simulations based on the perturbation approach initiated by Rice (1985) have provided valuable insights on the toughening of perfectly brittle materials by heterogeneities (Gao and Rice, 1989; Lebihain, 2021). They showcase unparalleled numerical efficiency, as they rely on order reduction techniques. Indeed, these models require only meshing of the 1D crack front to model 3D rupture. Yet, they build on a first-order expansion of the energy release rate with respect to the front deformation, and overlook the impact of geometrical nonlinearities arising from the front distortion. Higher-order theories are available (Leblond et al., 2012; Lebihain et al., 2023), but their practical implementation in a numerical code is still missing.
Objectives: You will develop a reduced-order numerical method to simulate the propagation of a planar crack in a heterogeneous material from the meshing of the crack front only. This method builds on an energetic approach to fracture mechanics (Francfort and Marigo, 1998). Equilibrium front positions are calculated by minimizing the sum of a potential energy, estimated asymptotically through the LEFM perturbation theory, and a dissipated energy, set by the fracture energy field. It will be implemented in Python using PETSc for optimization and JAX for automatic differentiation. You will benchmark your algorithm on archetypal cases for which analytical solutions are known. You will conduct hundreds of simulations of heterogeneous crack growth to investigate the impact of microstructural heterogeneities on the macroscopic fracture energy.
Growth opportunities: You will be part of Navier lab, an international research laboratory dedicated to the mechanics and physics of materials, structures and geomaterials. You will learn forefront concepts in theoretical fracture mechanics. You will learn to solve variational problems use optimization algorithms with Python and PETSc. You will receive support to present your work in front of a scientific audience, and write applications for academic positions.
Job opportunities: This internship is part of the 4-year project DURABLE funded by the French National Research Agency, which aims at designing tough and strong quasi-brittle composites through multiscale patterning. The successful candidate will be ideally positioned to apply for a (fully funded) Ph.D. position that will be opened next summer in the group.
Potential candidates must have a solid background in solid mechanics,
applied physics and mathematics, computational sciences, or a similar
discipline. They must have prior experience in programming, and possess
fluency in English, both spoken and written. Some knowledge of fracture
mechanics is a plus, but not mandatory.
Interested candidates should apply on this platform: Link.