PhD position: Size-sensitive strategies for the multiscale design of fracture-resistant heterogeneous materials
- Post by: Mathias Lebihain
- 2 December 2024
- No Comment
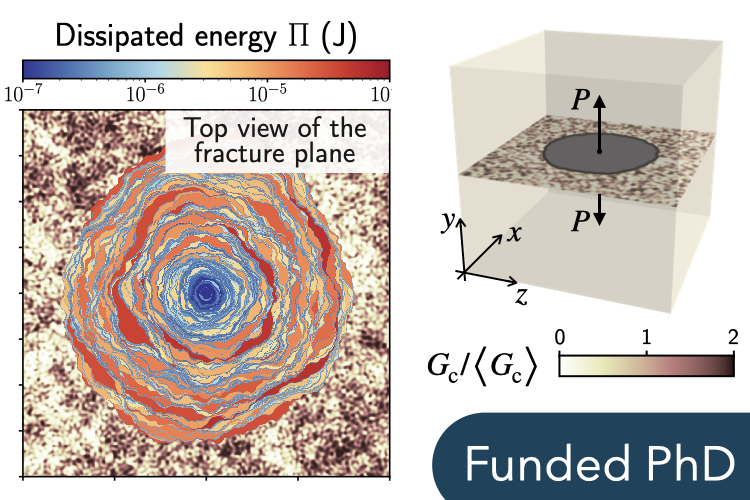
Context: Engineering materials, such as ceramics or concrete, often exhibit a complex microstructure characterized by multiple scales of heterogeneities, from the nanoscale (1~nm) up to the mesoscale (1~cm). Despite this microstructural complexity, they rarely combine high tensile strength (capacity to sustain stress without nucleating cracks) with large toughness (propensity to oppose crack propagation). Nature overcame this innate conflict through a hierarchical organization of biomaterials on multiple length scales. Over millions of years, biological materials have evolved microstructures with highly-structured interfaces, characterized by sharp fluctuations in stiffness, strength, and ductility. The principles underlying these multiscale reinforcement strategies have been successfully applied to create fracture-resistant bioinspired composites.
In the quest to emulate Nature’s designs, are we potentially overlooking alternative solutions? Modern challenges require optimizing the fracture properties of engineering materials based on constraints distinct from those found in Nature, such as environmental performance, fabrication process requirements, or resource availability. Nature’s blueprints, which result from complex evolutionary processes, may not be adequate to address sustainable, economical, or even geopolitical concerns. To address these new sets of constraints and usher in a new era of high-performance, durable composites, we must expand our focus beyond Nature’s own solutions, and explore design spaces more comprehensively. To this end, our goal is to pioneer a homogenization theory for tensile fracture properties. This framework will serve as a surrogate model for a fast screening of the vast compositional space of hierarchical composites.
Objectives: The position is part of the project DURABLE funded by the French National Research Agency. The goal of the PhD project is threefold. First, you will develop a numerical method that allows to simulate the propagation of a planar crack in a material containing thousands of heterogeneities. This method builds on cohesive-zone models that possess the necessary scale sensitivity to model crack propagation across scales (Marigo et al., IJSS, 2023). You will implement a discretized version of the variational formulation of cohesive fracture, where state equilibria are computed by minimizing the total energy using a bounded Newton conjugate gradient method with trust region, matrix-free implementation, and preconditioning. You will benchmark the algorithm against analytical solutions derived by Lebihain et al. (JMPS, 2022) and Roch et al. (PRL, 2023). Second, based on simulation results, you will develop a (semi-)analytical homogenization framework that predicts the apparent fracture properties of quasi-brittle composites from a statistical description of their microstructure at multiple hierarchical scales. Third, using this framework as a surrogate model, you will craft novel patterning strategies for composite design, depending on the scale of the inclusions with respect to that of the damage processes.
Opportunities for growth: You will be part of Navier lab, an international research laboratory dedicated to the mechanics and physics of materials, structures and geomaterials. You will learn forefront concepts in theoretical fracture mechanics. You will learn variational calculus to solve mechanical equilibrium perturbatively in presence of fluctuations/heterogeneities. You will learn to select and use optimization algorithms to solve variational problems in solid mechanics. You will receive support to write scientific articles, present your work in international conferences, and write research proposals to get your own grants/funding.
Candidate profile: Potential candidates must have a solid background in solid mechanics, applied physics and mathematics, computational sciences, or a similar discipline. They must have prior experience in programming, and possess fluency in English, both spoken and written. Some knowledge of fracture mechanics is a plus, but not mandatory.
Supervision: Dr. Mathias Lebihain (École des Ponts – Google Scholar), Prof. Laurent Brochard (École des Ponts – Google Scholar) and Prof. Djimédo Kondo (Sorbonne Université – Google Scholar)
How to apply: Interested candidates can apply on the ABG platform: Link
or email Dr. Mathias Lebihain (mathias.lebihain@enpc.fr) with:
- an updated CV;
- an academic transcript/list of courses completed, including grades;
- a summary of your past research, career goals, and their relevance to the job description (do it yourself, we want to hire you, not ChatGPT);
- the names and contact details of 1-2 references/mentors/past supervisors.
More details on the position and application process here: Link.


