The team develops various numerical methodologies as well as open-source libraries as part of its diverse research activities, such as multiscale modeling, structural analysis and optimization, the development of constitutive laws, and more.
Structural optimization
Jérémy Bleyer, Michaël Peigney, Romain Mesnil, Leyla Mourad (PhD), Hugo Masson (PhD)
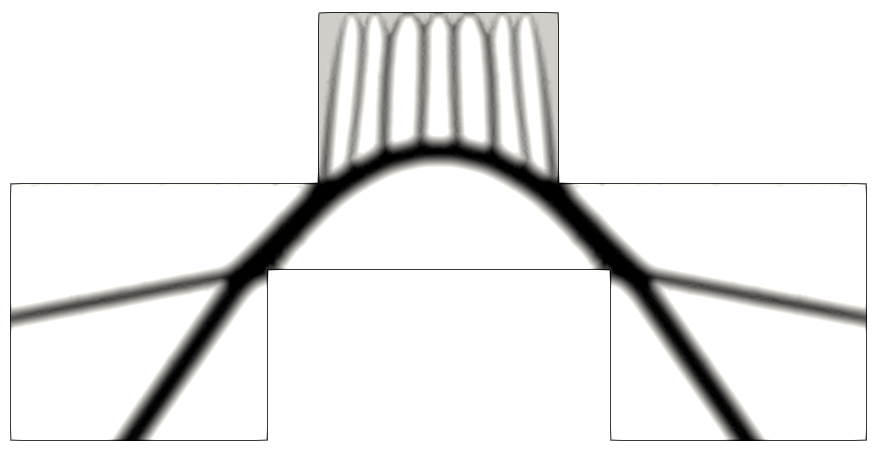
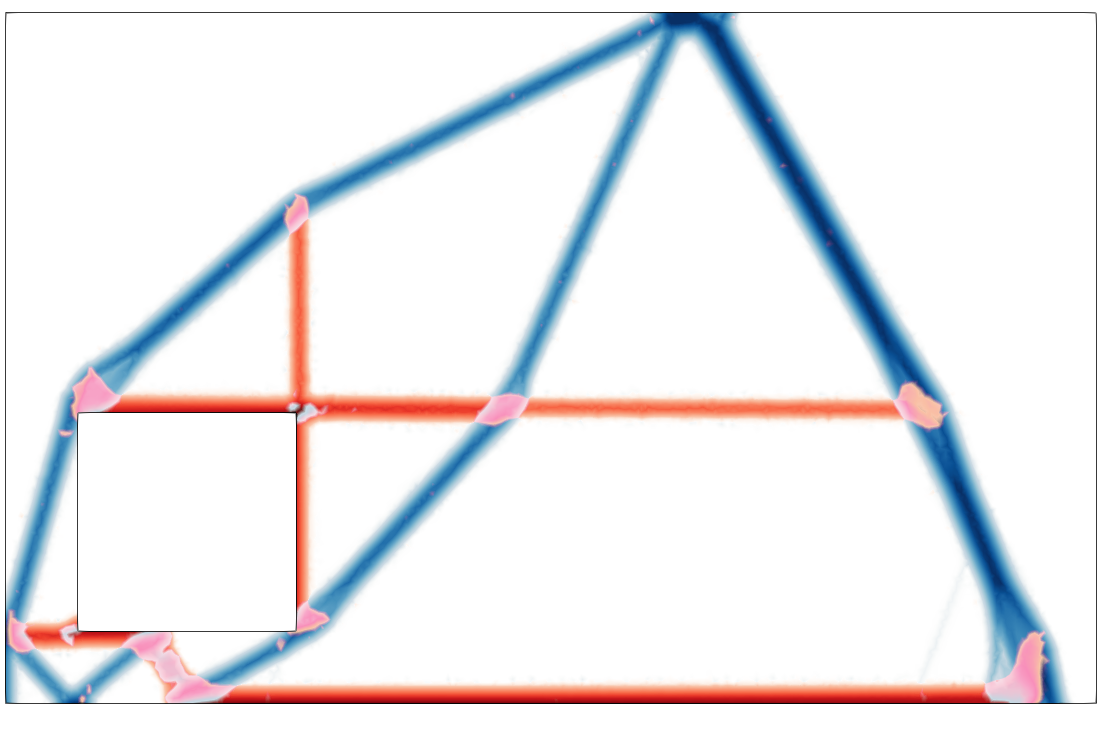
The team focuses on developing new approaches for finding optimal shapes for structures. Notably, we proposed an original formulation to maximize the ultimate load-carrying capacity of a structure. The proposed approach is an extension of limit analysis methods and relies on convex optimization tools to address cases of materials with no tensile strength, such as masonry, or anisotropic reinforced materials. This work has enabled the automatic generation of strut-and-tie models used in the design of reinforced concrete structures, paving the way for numerous extensions to other types of constitutive laws and the search for optimal vaults in curved structures.
Current work also focuses on accounting for uncertainties in topology optimization formulations, such as those inherent to additive manufacturing processes or those related to the loading conditions for which the structure is optimized.


Références
- Mourad, L., Bleyer, J., Mesnil, R., Nseir, J., Sab, K., & Raphael, W. (2021). Topology optimization of load-bearing capacity. Structural and Multidisciplinary Optimization, 64(3), 1367-1383.
- Mourad, L., Bleyer, J., Mesnil, R., Nseir, J., Sab, K., & Raphael, W. (2024). Multi-material topology optimization of structural load-bearing capacity using limit analysis.
Open-source software
Jérémy Bleyer
Coll. : Thomas Helfer (CEA), Jack S. Hale (Univ Luxembourg), Corrado Maurini (Sorbonne Université), Andrey Latyshev (PhD)
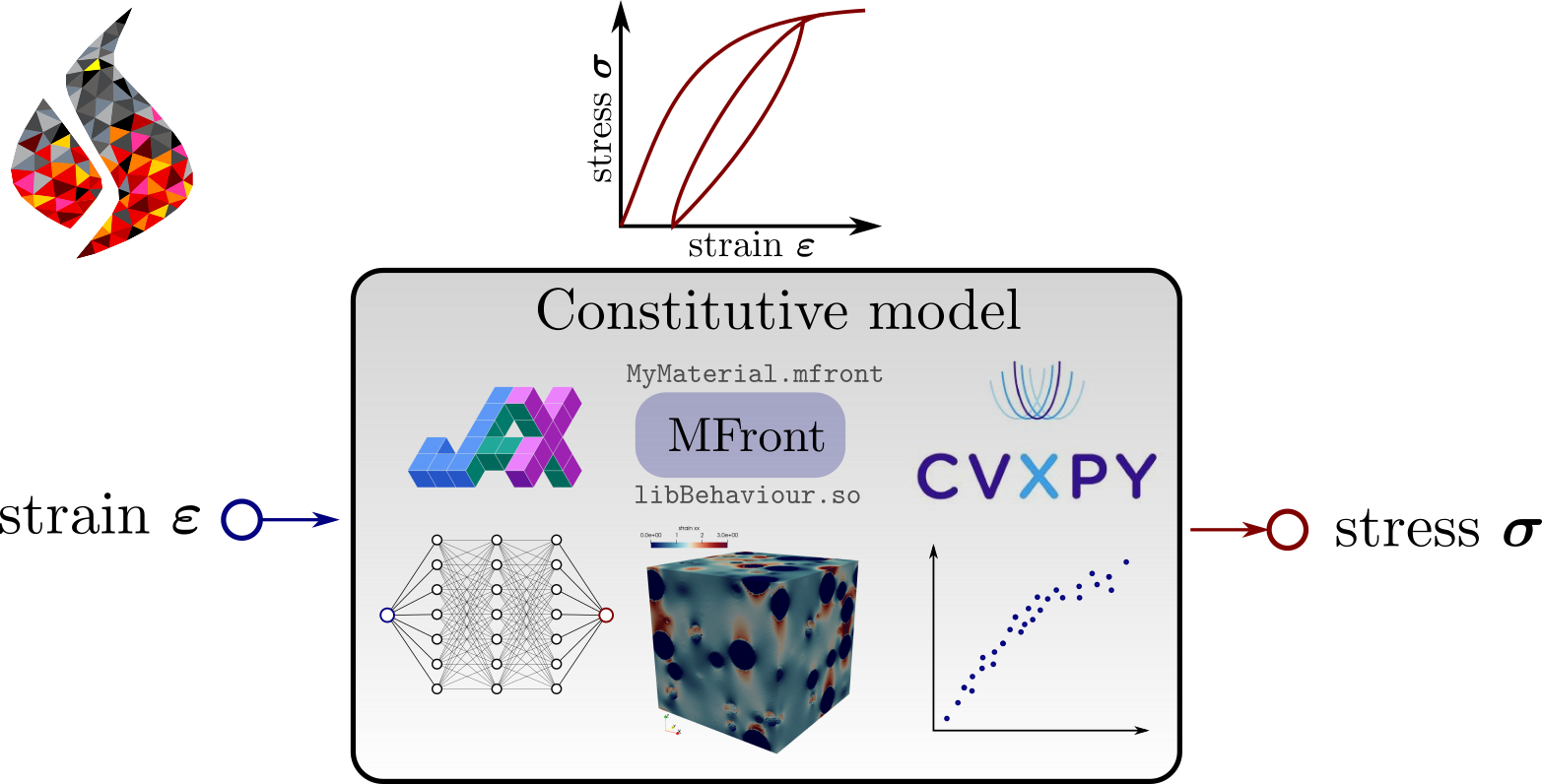
A part of the team’s numerical activities revolves around the overarching goal of automating nonlinear mechanics simulations using modern computational tools, such as the open-source finite element library FEniCS. One of the objectives is to develop a computational ecosystem for nonlinear mechanics within the FEniCS environment. More specifically, by leveraging FEniCS’ automation capabilities for formulating partial differential equations (PDEs), it is now possible to easily implement numerical solutions for complex nonlinear and multiphysics problems.
One of the main challenges in using FEniCS in a nonlinear mechanics context is the difficulty of natively handling implicit constitutive laws, which frequently arise in complex materials. To address this issue, we are developing the open-source package dolfinx_materials, which enables the integration of FEniCS with external libraries, including material behavior code generators such as MFront, machine learning libraries with automatic differentiation capabilities, and conic optimization solvers.
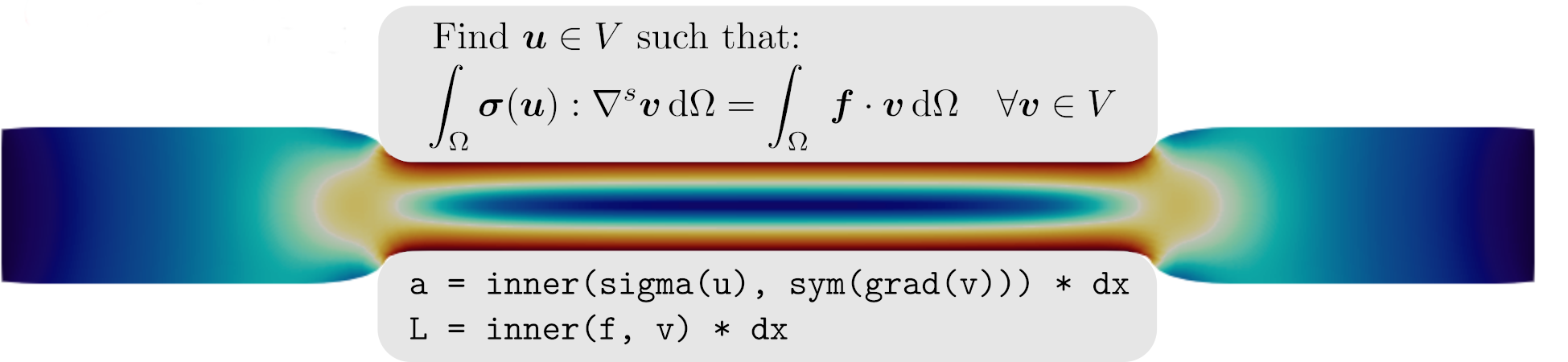
Références
- Bleyer, J. (2024). Numerical tours of Computational Mechanics with FEniCSx (v0.2). Zenodo. https://doi.org/10.5281/zenodo.13838486
- Bleyer, J. (2024). dolfinx_materials: A Python package for advanced material modelling (v0.3.0). Zenodo. https://doi.org/10.5281/zenodo.13882184
- Latyshev, A., Bleyer, J., Maurini, C., & HALE, J. (2024). Expressing general constitutive models in FEniCSx using external operators and algorithmic automatic differentiation.
Machine learning
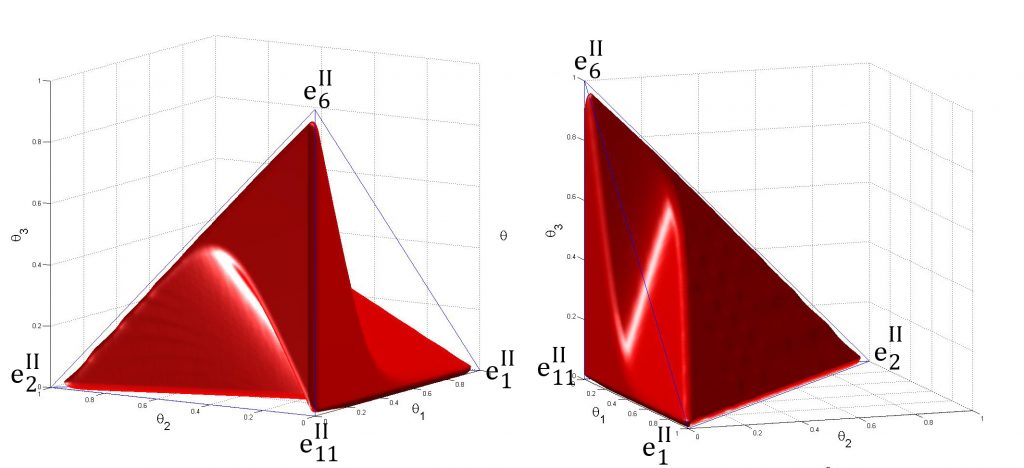
Artificial intelligence is increasingly being used in mechanics. One application involves learning complex constitutive laws. A machine learning technique based on Fourier decomposition has been developed and applied to three-phase nonlinear composites. Using AI to define constitutive laws offers a significant time-saving advantage for solving structural problems, particularly in shape optimization.
The question of bounds on the properties of composite materials remains open in the nonlinear case. A study investigated the optimality of established bounds for the effective conductivity of nonlinear composites in 2D, obtaining composite materials with properties close to the bounds, while still maintaining a simple microstructure that is easy to manufacture [Peigney 2022].

FFT-based homogenization of heterogeneous materials
Karam Sab, Jérémy Bleyer, Martin Dolbeau (PhD)
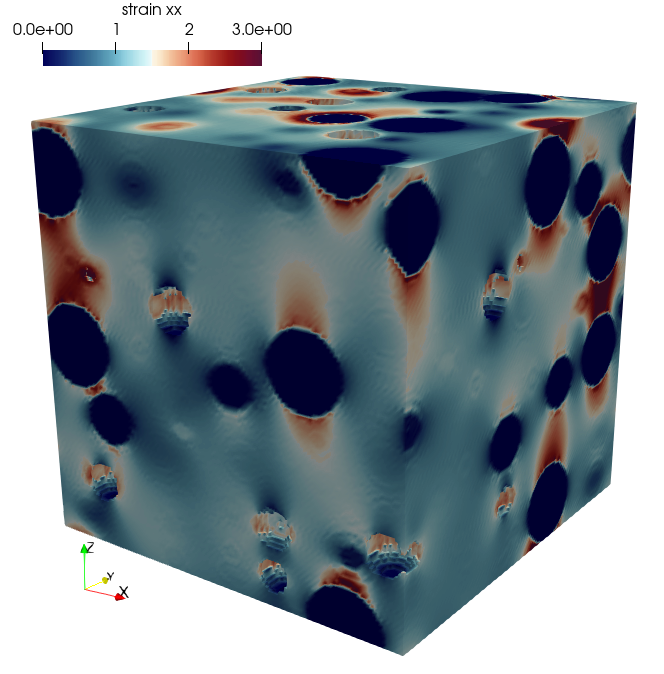
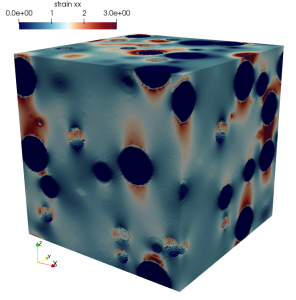
Moulinec and Suquet (1994) proposed, about thirty years ago, iterative algorithms based on FFT for the homogenization of periodic heterogeneous materials. However, in the presence of high contrasts, these algorithms struggle to converge. Although their efficiency has been improved by numerous studies since, they remain unable to handle infinite contrasts.
Recently, we proposed a new algorithm, inspired by the work of Eyre and Milton (1999), which effectively handles doubly infinite contrasts, i.e., microstructures containing simultaneously a heterogeneous matrix, infinitely rigid inclusions, and pores.
Références
- Sab, K., Bleyer, J., Brisard, S., & Dolbeau, M. (2024). An FFT-based adaptive polarization method for infinitely contrasted media with guaranteed convergence. Computer Methods in Applied Mechanics and Engineering, 427, 117012.
-
Sab, K., & Bleyer, J. (2023, June). An Adaptive Version of the Eyre-Milton Solution Scheme for FFT-Based Homogenization of Composites. In International Conference on Continuum Models and Discrete Systems (pp. 143-153). Cham: Springer Nature Switzerland.


