Réduction de la viscosité d’une huile par incorporation d’air
Romain Morini (Postdoc IFSTTAR 01/09/2014 au 31/12/2015), Laurent Tocquer, Xavier Chateau, Olivier Pitois, Guillaume Ovarlez (actuellement au LOF, Bordeaux)
Peut-on utiliser des bulles d’air pour abaisser temporairement la viscosité d’un liquide ? Il s’agit en fait d’un problème générique, dont la réponse est a priori connue depuis les années 1930, grâce aux travaux de Taylor : la viscosité relative d’une suspension de bulles dans un liquide visqueux dépend du nombre capillaire Ca = GηoRb /σ , formé avec le gradient de vitesse G qui caractérise l’écoulement, la viscosité ηo du liquide suspendant, le rayon de la bulle non déformée Rb et la tension de surface σ. La modélisation de ce problème a été proposée dès les années 1970 (Frankel & Acrivos par exemple). En revanche, la validation expérimentale de cette modélisation n’existait pas du fait de problèmes majeurs dans les travaux réalisés jusqu’alors : taille de bulles non-contrôlée, plage de valeurs trop limitée pour le paramètre Ca, précision de mesure rhéologique insuffisante.
Nous avons cherché à mesurer précisément cet effet, ce qui nous a conduit à mettre au point un dispositif expérimental basé sur des techniques milli-fluidiques. Les résultats obtenus ont permis, et ce pour la première fois, de discriminer les modélisations les plus efficaces pour décrire la viscosité des suspensions de bulles en fonction du nombre capillaire Ca et de la fraction volumique de bulles d’air Φ (voir la figure ci-dessous).
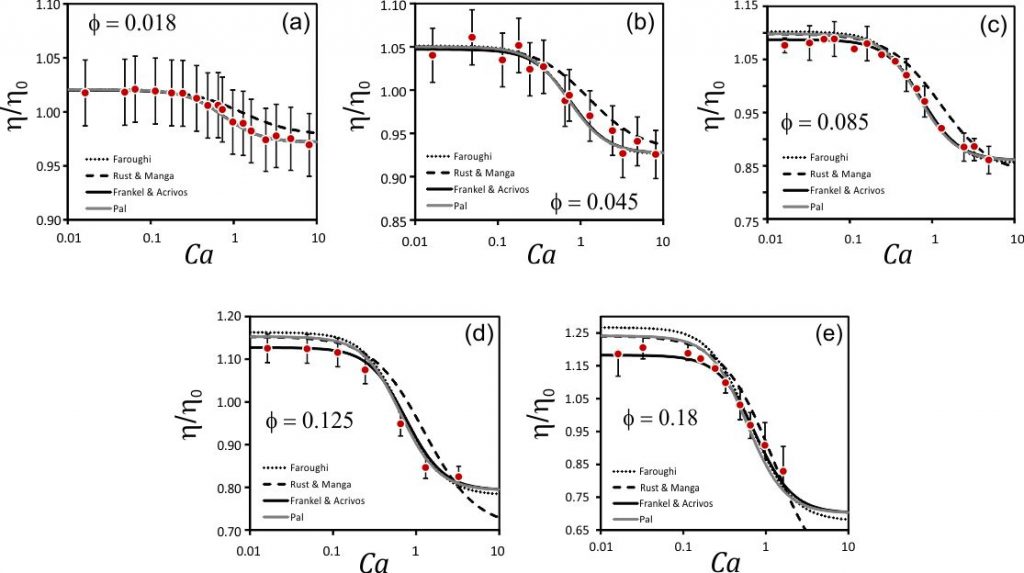
Figure : Viscosité apparente adimensionnée, η / η0, mesurée pour des suspensions de bulles à la fraction volumique Φ en fonction du nombre capillaire Ca. Les prédictions de plusieurs modèles théoriques sont présentées pour comparaison.
Publications
R. Morini, X. Chateau, G. Ovarlez, O. Pitois, L. Tocquer, Steady shear viscosity of semi-dilute bubbly suspensions, Journal of Non-Newtonian Fluid Mechanics 264 (2019) 19–24
R. Morini, X. Chateau, G. Ovarlez, O. Pitois, L. Tocquer, Viscous friction of squeezed bubbly liquid layers, Soft Matter, 2018, 14, 8372-8377
Comportement rhéologique d’une pâte aérée
Lucie Ducloué (Thèse Cifre Saint-Gobain, soutenue le 09/09/2014), Xavier Chateau, Olivier Pitois, Guillaume Ovarlez (actuellement au LOF, Bordeaux), Julie Goyon
L’étude présentée ci-dessus concerne la rhéologie d’un liquide simple aéré, alors que de nombreux matériaux ont une rhéologie qui est intrinsèquement plus complexe. C’est par exemple le cas des pâtes, qui sont largement utilisées dans l’élaboration de matériaux, et dont le rhéogramme fait apparaître une contrainte seuil, τyo, au-dessus de laquelle le matériau s’écoule comme un liquide, alors que leur comportement est celui d’un solide (élastique) pour des valeurs inférieures de la contrainte appliquée. Comment cette rhéologie complexe est-elle modifiée par la présence de bulles ?
Cette problématique a été traitée dans l’équipe. Par un excellent contrôle et un découplage des différents paramètres de ces systèmes, nous avons pu préciser l’effet rhéologique des bulles dans la pâte. Nous montrons que la transition solide/liquide est pilotée par le nombre capillaire de Bingham Cay = τyoRb /σ , où Rb est le rayon des bulles et σ la tension de surface ; en particulier, pour Cay ≤ 0.1, la contrainte seuil du matériau aéré τy(Φ) reste très proche de celle de la matrice (τyo) et ne dépend pas de la taille des bulles. Pour des contraintes bien inférieures à cette contrainte seuil, le matériau à un comportement élastique composé de l’élasticité capillaire des bulles et de celle de la matrice ; ces deux contributions sont pilotées par le nombre capillaire élastique, Caél = GoRb /σ , où Go est le module élastique de la pâte : plus les bulles sont grosses, plus le matériau apparaît « mou » (voir la figure ci-dessous).
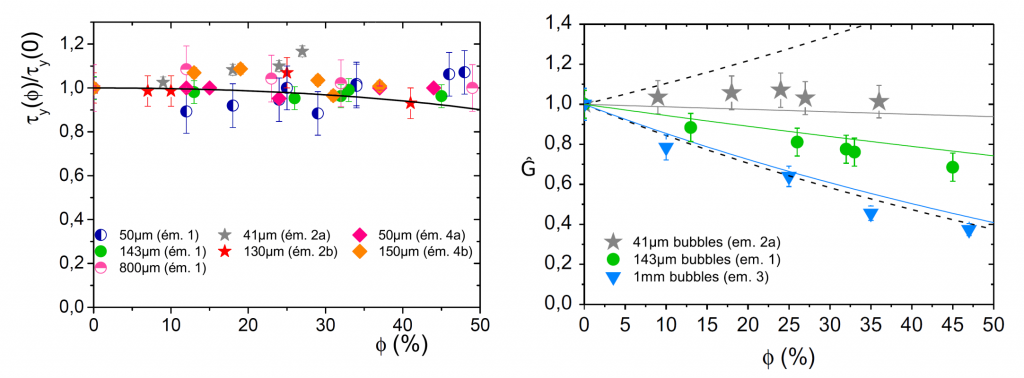
Des bulles d’air modifient la rhéologie d’une pâte. Gauche : Contrainte seuil des pâtes aérées divisée par la contrainte seuil du matériau en fonction de la fraction volumique d’air. De manière assez surprenante, cette contrainte réduite ne dépend pas de la taille des bulles. Droite : Lorsque la contrainte est inférieure à la contrainte seuil, le comportement de la pâte aérée est celui d’un solide élastique (la grandeur représentée est le module élastique de la pâte aérée divisée par le module élastique du matériau). On constate que cette fois-ci, le comportement dépend de la taille des bulles : plus elles sont grosses, plus le matériau aéré apparaît mou ; pour des bulles suffisamment petites, le module est légèrement renforcé par la présence des bulles.
Publications
L. Ducloué, O. Pitois, J. Goyon, X. Chateau, G. Ovarlez, Rheological behaviour of suspensions of bubbles in yield stress fluids, Journal of Non-Newtonian Fluid Mechanics 215 (2015) 31–39
L. Ducloué, O. Pitois, J. Goyon, X. Chateau, G. Ovarlez, Coupling of elasticity to capillarity in soft aerated materials, Soft Matter, 2014, 10, 5093–5098
L. Ducloué, O. Pitois, J. Goyon, X. Chateau, G. Ovarlez, Yielding and flow of foamed metakaolin pastes, Colloids and Surfaces A: Physicochem. Eng. Aspects 513 (2017) 87–94
Moussage des fluides complexes : dynamique de la formation des bulles dans des fluides à seuil en géométries confinées
Benoît Laborie (Thèse LABEX MMCD, soutenue le 01/10/2015), Elise Lorenceau (CNRS, NAVIER – actuellement LiPhy à Grenoble), Florence Rouyer (UPEM, NAVIER), Dan Angelescu (ESIEE, ESYCOM actuellement FLUIDION )
Beaucoup de matériaux moussés résultent d’un mélange d’une mousse avec un fluide à seuil, nous avons cherché à produire une mousse directement par l’inclusion d’air dans une émulsion à partir de système classique utilisé en micro-fluidique telle qu’une jonction en T et un dispositif « flow focusing » mais d’échelle milli-fluidique.
La pression de gaz est imposé à l’entrée principale du dispositif et le fluide à seuil est injecté à débit constant à l’entrée secondaire (transverse à l’écoulement principal). Nous avons identifié un mécanisme robuste de production de bulles lorsque la contrainte seuil dépasse la pression capillaire. La fréquence maximale de production de bulle en régime stationnaire est imposé par le temps minimum de fractionnement de l’air fixé par le rapport du volume de la jonction et du débit de fluide à seuil [1]. Nous avons alors identifié les différents modes d’écoulement des mousses de fluides à seuil dans ces canaux en fonction de la pression de gaz imposé [2]. Un régime stationnaire peut-être atteint pour un dispositif à pression de gaz imposée à condition que la pression soit régulée dynamiquement aux premiers instants pour compenser non seulement la perte de charge hydrodynamique lié à l’injection d’air mais aussi au dépôt de fluide sur les parois [3]. L’étude du dépôt de fluide à seuil dans un conduite cylindrique montre que l’épaisseur déposée peut être plus importante pour un fluide à seuil de type Bingham que pour un fluide Newtonien et que l’épaisseur augmente avec la valeur du seuil [4]. Ce travail a également fait apparaître l’importance du glissement des fluides à seuil, qui a fait l’objet de la thèse de Xio Zhang (soutenue 12/10/2018, voir thème Rheology of pastes, and complex fluids).
Publications
[1] B. Laborie, F. Rouyer, D. E. Angelescu, and E. Lorenceau (2015), “Bubble Formation in Yield Stress Fluids Using Flow-Focusing and T-Junction Devices”, Physical Review Letters, 114, 204501.
[2] B. Laborie, F. Rouyer, D.E. Angelescu, E. Lorenceau (2016), “Yield-stress fluids foams: flow patterns and controlled production in T-junction and flow-focusing devices “, Soft Matter 12(46), 9355.
[3] B. Laborie, F. Rouyer, D. Angelescu, E. Lorenceau (2016), “On the stability of the production of bubble in Yield-stress Fluid using Flow-focusing and T-junction devices” , , Physics of Fluid 28(6), 063103 (2016).
[4] B. Laborie, F. Rouyer, D.E. Angelescu, E. Lorenceau(2017), “Yield-stress fluid deposition in circular channels", Journal of Fluid Mechanics 818, 838-851.

Un fluide à seuil (YSF) est injecté à débit constant (Q) perpendiculairement à une canalisation où la pression (P) ou le débit (Gg) de gaz est imposée en entrée. Un régime de production stationnaire de bulles peut être atteint. Un mousse est obtenue à la sortie du dispositif.

