L’équipe développe différentes méthodologies numériques ainsi que des bibliothèques open-source dans le cadre de ses différentes activités de recherche telles que les changements d’échelle, le calcul de structures et leur optimisation, le développement de lois de comportement, etc.
Optimisation structurale
Jérémy Bleyer, Michaël Peigney, Romain Mesnil, Leyla Mourad (PhD), Hugo Masson (PhD)
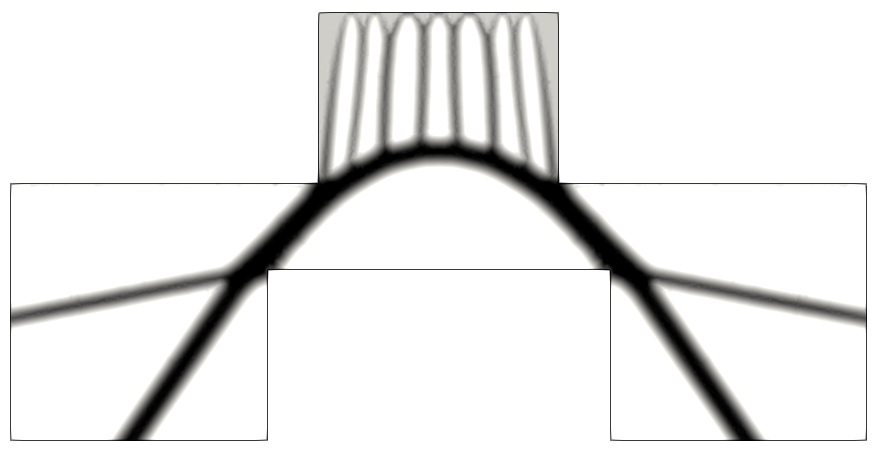
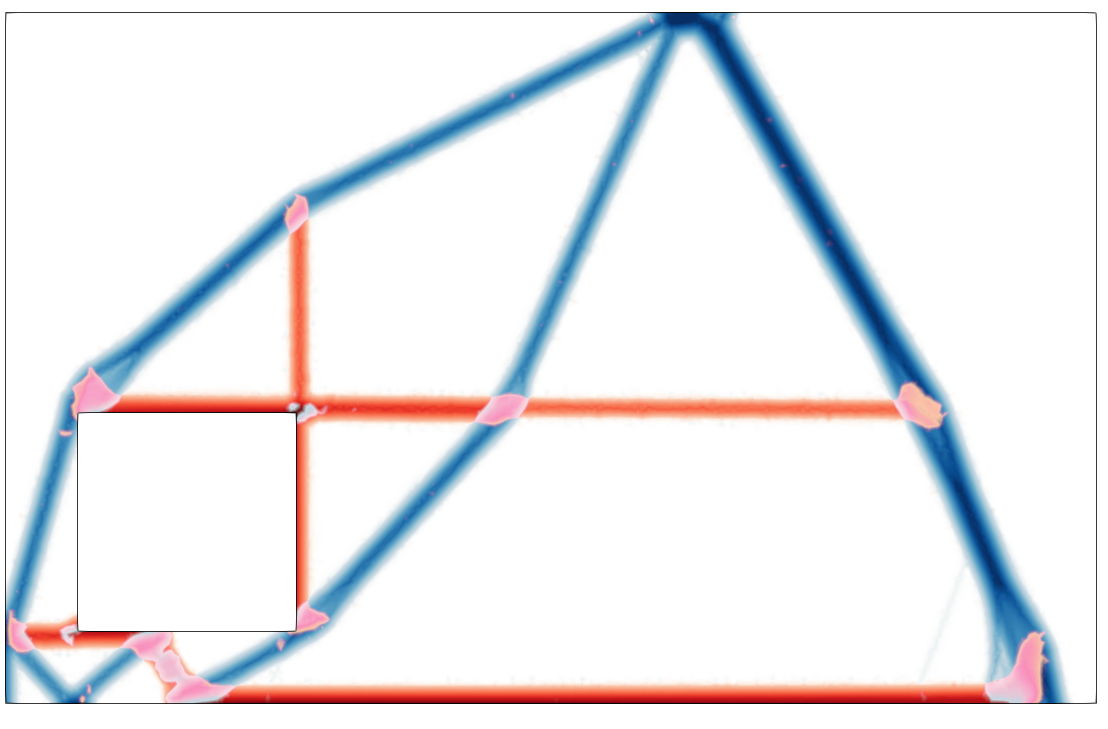
L’équipe s’intéresse au développement de nouvelles approches concernant la recherche de formes optimales pour les structures. Nous avons notamment proposé une formulation originale pour maximiser la capacité portante ultime d’une structure. L’approche proposée consiste ainsi en une extension des approches d’analyse limite et repose sur des outils d’optimisation convexe pour traiter des cas de matériaux sans résistance à la traction, comme la maçonnerie, ou des matériaux anisotropes renforcés. Ce travail a permis la génération automatique de modèles de bielles et tirants utilisés pour la conception de structures en béton armé, ouvrant la voie à de nombreuses extensions pour d’autres types de lois de comportement et la recherche de voûtes optimales dans les structures courbes.
Les travaux actuelles s’intéressent également à la prise en compte d’incertitudes dans les formulations d’optimisation topologique telles que celles inhérentes aux procédés de fabrication additive ou encore celles liées au chargement pour lequel la structure est optimisée.


Références
- Mourad, L., Bleyer, J., Mesnil, R., Nseir, J., Sab, K., & Raphael, W. (2021). Topology optimization of load-bearing capacity. Structural and Multidisciplinary Optimization, 64(3), 1367-1383.
- Mourad, L., Bleyer, J., Mesnil, R., Nseir, J., Sab, K., & Raphael, W. (2024). Multi-material topology optimization of structural load-bearing capacity using limit analysis.
Développement de logiciels libres
Jérémy Bleyer
Coll. : Jack S. Hale (Univ Luxembourg), Corrado Maurini (Sorbonne Université), Andrey Latyshev (PhD)
Une partie de des activités numériques de l’équipe s’articule autour de l’objectif global d’automatiser les simulations de mécanique non linéaire en utilisant des outils de calcul modernes tels que la librairie open-source de calcul aux éléments finis FEniCS. Un des objectifs est de développer un écosystème de calcul pour la mécanique non linéaire au sein de l’environnement FEniCS. Plus précisément, en exploitant les capacités d’automatisation de FEniCS pour formuler des équations aux dérivées partielles (EDP), il est désormais possible d’implémenter facilement des solutions numériques pour des problèmes complexes non linéaires et multiphysiques.
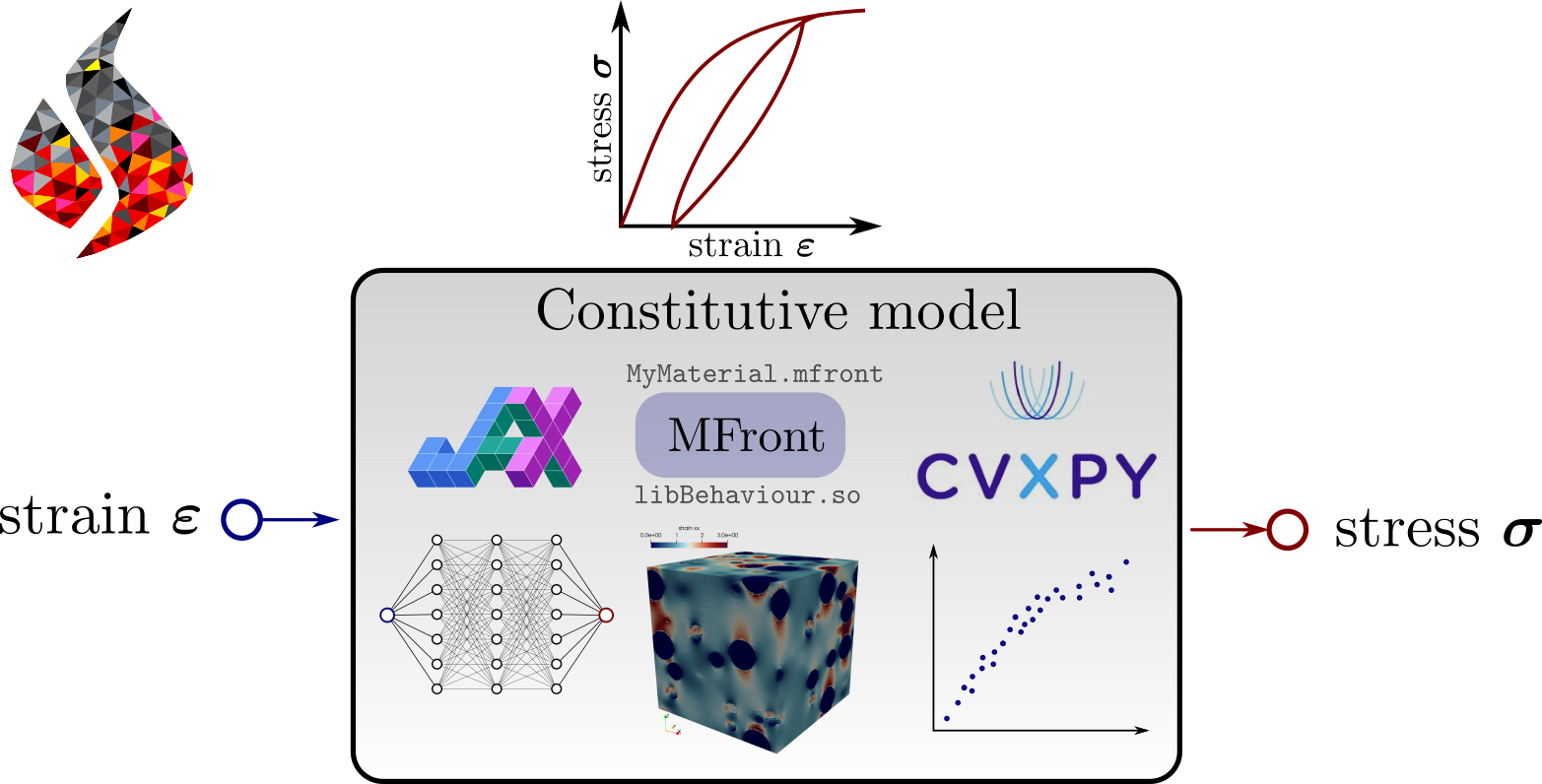
L’un des principaux défis de l’utilisation de FEniCS dans un contexte de mécanique non linéaire est la difficulté de traiter de manière native les lois de comportement implicites, qui apparaissent fréquemment pour les matériaux complexes. Pour répondre à ce problème, nous développons le package open-source dolfinx_materials permettant d’intégrer FEniCS avec des bibliothèques externes, notamment des générateurs de code pour les comportements des matériaux tels que MFront, des bibliothèques d’apprentissage automatique avec des fonctionnalités de différenciation automatique, et des solveurs d’optimisation conique.
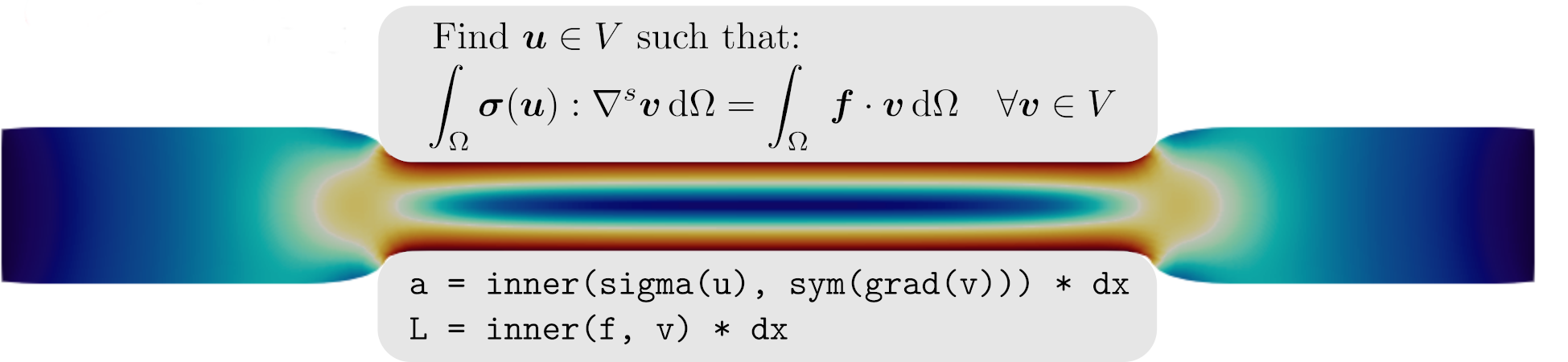
Références
- Bleyer, J. (2024). Numerical tours of Computational Mechanics with FEniCSx (v0.2). Zenodo. https://doi.org/10.5281/zenodo.13838486
- Bleyer, J. (2024). dolfinx_materials: A Python package for advanced material modelling (v0.3.0). Zenodo. https://doi.org/10.5281/zenodo.13882184
- Latyshev, A., Bleyer, J., Maurini, C., & HALE, J. (2024). Expressing general constitutive models in FEniCSx using external operators and algorithmic automatic differentiation.
Méthodes par apprentissage
Sample Text
Homogénéisation par FFT des matériaux hétérogènes
Karam Sab, Jérémy Bleyer, Martin Dolbeau (PhD)
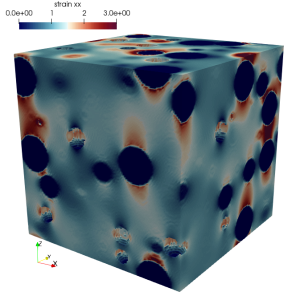
Moulinec et Suquet (1994) ont proposé, il y a une trentaine d’années, des algorithmes itératifs basés sur la FFT pour l’homogénéisation des matériaux hétérogènes périodiques. Cependant, en présence de contrastes élevés, ces algorithmes ont du mal à converger. L’efficacité de ces algorithmes a été améliorée depuis par de nombreux travaux sans pouvoir gérer des contrastes infinis.
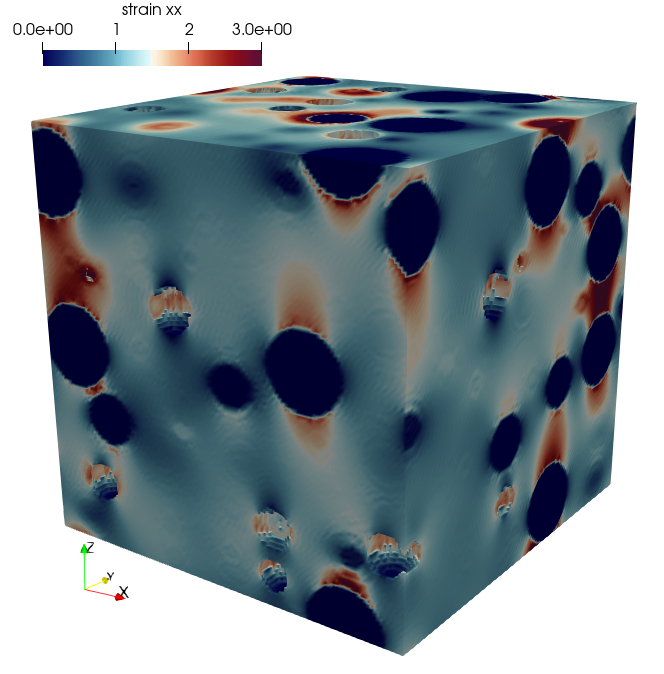
Nous avons proposé récemment un nouvel algorithme, s’inspirant de celui de Eyre et Milton (1999), qui permet de traiter efficacement des contrastes doublement infinis, c’est-à-dire des microstructures contenant simultanément une matrice hétérogène, des inclusions infiniment rigides et des pores.
Références
- Sab, K., Bleyer, J., Brisard, S., & Dolbeau, M. (2024). An FFT-based adaptive polarization method for infinitely contrasted media with guaranteed convergence. Computer Methods in Applied Mechanics and Engineering, 427, 117012.
-
Sab, K., & Bleyer, J. (2023, June). An Adaptive Version of the Eyre-Milton Solution Scheme for FFT-Based Homogenization of Composites. In International Conference on Continuum Models and Discrete Systems (pp. 143-153). Cham: Springer Nature Switzerland.

