The steady shear viscosity of bubbly suspensions is known to depend upon the suspending fluid viscosity, the bubble volume fraction and a dimensionless number (the capillary number) accounting for the deformability of the bubbles under viscous stress. However, experimental data on bubbly suspensions in the literature were scarce and presented two main shortcomings: (i) the studied systems were polydisperse, which leaded to arbitrariness in the definition of a capillary number, and (ii) there was a lack of data for capillary numbers of order unity, where bubbles are slightly deformable. This leaded to the absence of clear conclusion about the relevance of the existing theoretical models.
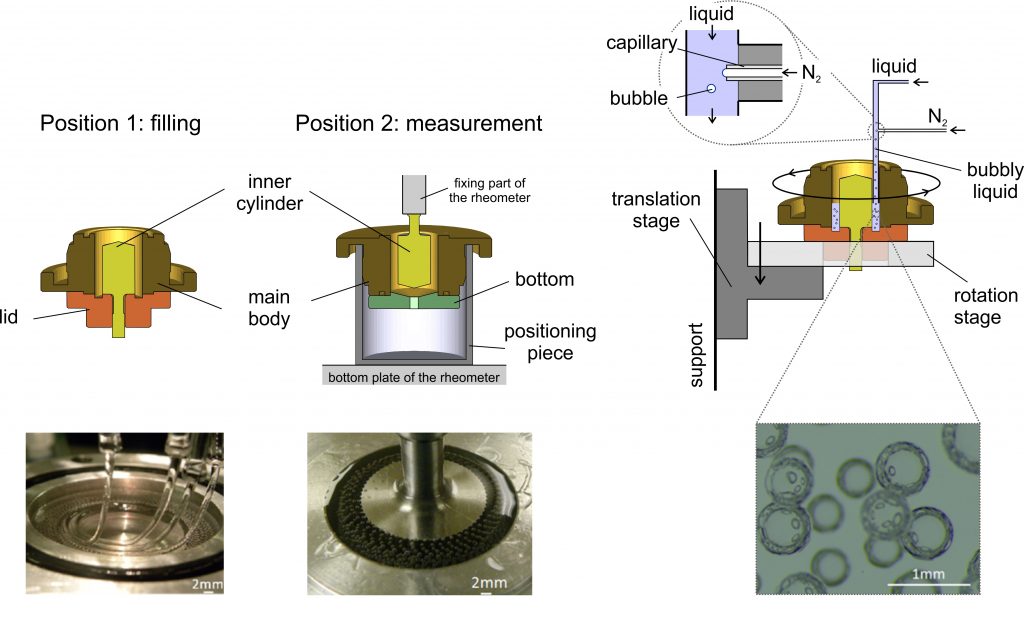
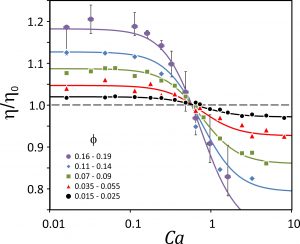
In order to make significant progress, an original device was designed to produce monodisperse suspensions of bubbles in a highly viscous Newtonian fluid. The steady shear viscosity of the bubbly suspensions was measured in the dilute and semi-dilute concentration regimes (volume fraction of bubbles between 2% and 18%) using a Couette geometry with a 20-bubbles-wide gap, for capillary numbers ranging between 0.01 and 10. The new obtained data were shown to be much more accurate than data previously reported in the literature. Experimental data are in very good agreement with the model of Frankel and Acrivos (1970), originally developed for dilute suspensions, in the whole range of studied volume fractions.
Related Paper:
– Steady shear viscosity of semi-dilute bubbly suspensions, R. Morini, X. Chateau, G. Ovarlez, O. Pitois, L. Tocquer, Journal of non-Newtonian fluid mechanics (2019) 264, 19-24


