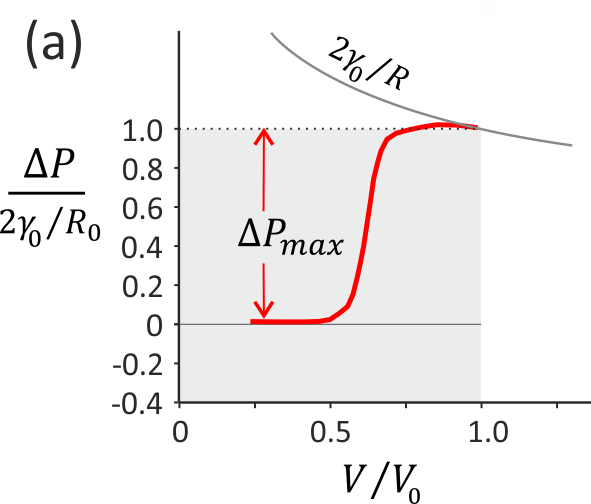
We studied the collapse of millimeter drops (radius R) coated with micrometer-sized spherical PS particles (radius a). The drops were forced to shrink in size through progressive removal of their bulk liquid while their internal pressure ∆P was measured. A typical result is presented in figure a: below a given volume Vo (and a corresponding drop radius R0) the drop pressure deviates from the expected Laplace pressure (2γo)⁄R and instead decreases down to vanishing values. This transition was attributed to the strong particle interactions induced by the contraction of the interface during drop shrinkage. The pressure value at collapse was measured to be close to zero, which means that the mechanical equilibrium of the drop was maintained provided the applied (forcing) pressure was below ∆Pmax such that ∆Pmax⁄(2γo)⁄Ro)≈ 0.8-0.9. This result can be understood as follows: Any bulk pressure reduction (with respect to the capillary pressure 2γo⁄Ro induces an increase of the surface pressure Π within the particle monolayer. Equivalently, the effective surface tension γ=γo-Π decreases when the drop shrinks. When γ≈0 there is strong compressive stress in the monolayer but the internal pressure is now too small to maintain the spherical shape, leading the destabilization (collapse) of the drop.
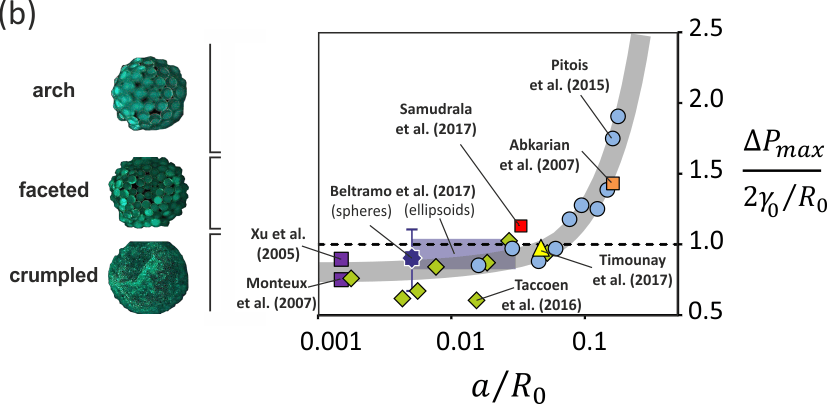
Whereas ∆Pmax(2γo⁄Ro)≈ 0.9 was measured for the smallest a⁄R values, the armor strength was found to increase significantly for a⁄Ro > 0.1, which means that negative internal pressures can be reached in this regime (the free interface is negatively curved between the particles). Actually, ∆Pmax⁄(2γo⁄Ro)≈ 2 for a⁄Ro ≈ 0.2, which means that the internal pressure reaches -2γo⁄Ro at collapse. We stress that all the results from literature can be gathered on the same graph by plotting the reduced collapse pressure ∆Pmax⁄(2γo⁄Ro) (which is equivalent to Π⁄γo) as a function of a⁄Ro (see figure b). We show here that all the data can be described as follows: ∆Pmax ⁄(2γo⁄Ro) )≈ 0.8-1 for a⁄Ro ≲ 0.1 and ∆Pmax ⁄(2γo⁄Ro) > 1 for a⁄Ro > 0.1.
Dedicated physical models have been proposed to describe both the collapse pressure and the crumpled shape of the drop/bubble at collapse. The basic idea is that as stress increases in the monolayer due to interface contraction, particles are pushed out of the plane by forces at contact, resulting in an accordion or a sinusoidal shape for the interface. In the same time capillary restoring forces restrain those motions and set the magnitude of the elastic modulus. Moreover, it has been suggested that out-of-plane motions are prevented for larger size ratios. The underlying mechanism is the entanglement of particles through their contact network at the curved interface, leading to the formation of stable particle arches. This mechanism has been shown to modify the armor shape at collapse with respect to the crumpled shape observed for a⁄Ro ≪ 0.1: faceted shapes were observed for a⁄Ro ≈ 0.1 and spherical (i.e. undeformed until sudden collapse) shapes were observed for a⁄Ro ≈ 0.2.
Related Papers:
– On the collapse pressure of armored bubbles and drops, O. Pitois, M. Buisson, X. Chateau, European Physical Journal E (2015) 38, 132
– Rheology of particulate rafts, films, and foams, O. Pitois, F. Rouyer, Current Opinion in Colloid & Interface Science (2019) 43, 125-137.

